REPRESENTACIÓN DE UN SISTEMA DISCRETO MEDIANTE SU RESPUESTA AL IMPULSO
Convolución discreta
Habíamos visto que una forma de representar un sistema es a través de su respuesta en frecuencia o función transferencia; existe otra forma de caracterizar un sistema, en el dominio del tiempo y es mediante su respuesta al impulso. Es decir:

Cuando x[n]= δ [n], la salida y[n], la cual llamaremos h[n], será la respuesta al impulso o respuesta impulsiva. Como el sistema es lineal e invariante en el tiempo, la respuesta a
x[n] = Aδ[n-k] será Ah[n-k]
Esto nos permitirá conocer la respuesta a cualquier entrada arbitraria x[n] ya que siempre podemos expresar a x[n] como:
x[n] = ∑ Ak.δ[n-k]
y[n] = ∑ Ak.h[n-k]
Esto se conoce como convolución discreta o suma de convolución entre la entrada (definida por los Ak) y la respuesta impulsiva h[n]
y[n] = x[n]* h[n]
La convolución discreta tiene las siguientes propiedades:
1. Conmutatividad:
x[n]*y[n]= y[n]*x[n]
(x[n]*y[n]*w[n] = x[n]*(y[n]*w[n])
Esto es aplicable por ejemplo si queremos determinar la salida para la cascada de 2 sistemas con respuesta impulsiva h1[n] y h2[n] respectivamente. Esta propiedad permite concluir que el orden de colocación de los sistemas no es importante.

(x[n]* h1[n])*h2[n] =(x[n]* h2[n])*h1[n]
3. Distributividad:
(x[n]+y[n])*w[n] = x[n]*w[n] + y[n]*w[n]
Esta propiedad nos permite determinar la salida cuando la señal de entrada pasa
por dos sistemas conectados en paralelo.
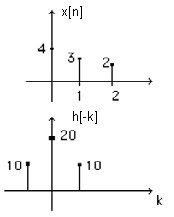
Ejemplo: Un sistema con respuesta h[n] es alimentado con una señal x[n], tal y como se muestra a continuación.
Determine la salida y[n] de dicho sistema mediante convolución.
Pasos para resolver la convolución discreta.
Para determinar estos valores se grafica dejando x[n] en su lugar y dibujando h[n-k] hacia la izquierda y derecha de x[n].
Como sigue a continuación:
Para que x[k].h[n-k] = 0, hacia la izquierda n+1<0
n < -1
n > 2+1
n>3
4.- Luego se deben multiplicar x[k].h[n-k], solo desplazando h[n-k] hacia la derecha. En este caso desde n= -1 hasta n = 3
Para n=-1
y[-1]= 4 x 10 = 40
Para n = 0
y[0]= 4 x 20 + 3 x 10= 110
Para n = 1
y[1]=4 x 10 + 3 x 20 + 2 x 10 = 120
Para n = 2
y[2]=3 x 10 + 2 x 20 = 70
Para n = 3










Hola profesora Gloria me parece muy bueno el material, el cual trararé de complementar con alguna otra información adicional que logre conseguir por internet. Muchas gracias. Nos seguiremos viendo
ResponderEliminarprofesora saludos es Yonder Casanova C.I. 16.595.575 g-002 telecomunicaciones
ResponderEliminaryurismar Guzmàn
ResponderEliminarC.I:20.696.753
Secciòn:001-d-ing en telecomunicaciones
hola buenas tardes profesora el material que publico es muy bueno
buenas tardes prof, esta es mi asistencia de la semana
ResponderEliminarBuenos dias
ResponderEliminarMaria K. Marquez G.
C.I.19.230.388
no puedo irme de este site sin , dejarle mis agradecimientos por subir esta información que para mi resulta valiosisima.
ResponderEliminarsoy estudiante de robotica y curso el ramo de procesamiento de señales,he tratado de encontrar informcion en todos lados respecto de suma de convolucion y no he encontrado un lugar donde me quede claro como acá, muchisimas gracias en verdad me ha sido de extrema ayuda.
bendiciones
santiago mandiola
Totalmente de acuerdo contigo Santiago
EliminarMuchas gracias!! Llevaba un año sin tocar convoluciones y este año para la asignatura Señales y Sistemas II de ingeniería de telecomunicación me hacía falta. Me ha recordado el concepto perfectamente! Muchas gracias de nuevo!
ResponderEliminarBuenas, soy estudiante de telecomunicaciones y estoy dando sistemas lti y convoluciones en este momento. La verdad, con esta explicación me ha quedado más claro que leyendo en algunos libros, donde profundizan demasiado y se ponen muy técnicos sin dejar muy clara la metodología para resolver esta clase de problemas. Por otro lado, es una pena que hayas limitado el artículo a las convoluciones discretas, dejando de lado las continuas. Aún así, muchísimas gracias por el material, me ha sido de gran utilidad, saludos!
ResponderEliminarhee profe y como desarrollo la expresion matematica... gracias
ResponderEliminarhol, me gustaría saber que es lo que pasa cuando la señal que se invierte para hacer la convolución no tiene ninguna delta en 0, es decir, a qué se le llama n...
ResponderEliminarHola Gloria, Soy Alberto Yánez Ing. Electrónico UNET egresado en 2009. Te queria preguntar en que libro puedo encontrar diagramas de respuestas impulso, que se relacionen con convolución, pero en términos de [n], por decir, algunas reglas que me especifiquen cual es la convolución, por ejemplo impulso[n]*escalon[n]= escalon[n]
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarGracias, me ayudó muchísimo. Atículos como este inspiran a hacer lo mismo.
ResponderEliminarMuchas Gracias. Por fin he entendido la dichosa convolución.
ResponderEliminargracias de verdad, entendí todo
ResponderEliminar