APLICACION DE LA TRANSFORMADA DE FOURIER AL CAMPO DE LAS COMUNICACIONES

PAGINA 1

PAGINA 2

PAGINA 3

PAGINA 4

PAGINA 5

PAGINA 6

PAGINA 7

CONTINUACION UNIDAD V

PAGINA 1

PAGINA 2

PAGINA 3

PAGINA 4

PAGINA 5

PAGINA 6

PAGINA 7

PAGINA 8

UNIDAD V. ANALISIS DE SISTEMAS EN EL DOMINIO DE LA FRECUENCIA UTILIZANDO LA TRANSFORMADA DE FOURIER

PAGINA 1

PAGINA 2

PAGINA 3

PAGINA 4

PAGINA 5

PROPIEDADES DE LA TRANSFORMADA DE FOURIER

PAGINA 1

PAGINA 2

PAGINA 3

PAGINA 4

PAGINA 5

PAGINA 6

PAGINA 7

PAGINA 8

INFORMACION PROXIMA CLASE

EL SABADO 11 DE JULIO BAJO LA INFORMACION DE LA CLASE

SERIES Y TRANSFORMADAS DE FOURIER

PAGINA 1

PAGINA 2

PAGINA 3

PAGINA 4

PAGINA 5

PAGINA 6

PAGINA 7

PAGINA 8

PAGINA 9

PAGINA 10

PAGINA 11

PAGINA 12

EJERCICIOS Y TRABAJO

Para el trabajo resolver los ejercicios: 1, 2.b, 3 y 4.b


Ejercicios

1. Hallar y(t)= x(t)* h(t)

2. Determine la señal de salida Y(t) para los siguientes circuitos, mediante ecuaciones diferenciales

2.a. VL (t) = L di(t)/dt

2.b. Ic(t) = C dV(t)/dt

3. Hallar y[n]=x[n]*h[n]


4. Determinar si los siguientes sistemas son lineales o no.

4.a. Si R1=R2.x(t)


4.b. y(t) = 2x(t) + 3

CONVOLUCION DISCRETA

REPRESENTACIÓN DE UN SISTEMA DISCRETO MEDIANTE SU RESPUESTA AL IMPULSO

Convolución discreta

Habíamos visto que una forma de representar un sistema es a través de su respuesta en frecuencia o función transferencia; existe otra forma de caracterizar un sistema, en el dominio del tiempo y es mediante su respuesta al impulso. Es decir:

Cuando x[n]= δ [n], la salida y[n], la cual llamaremos h[n], será la respuesta al impulso o respuesta impulsiva. Como el sistema es lineal e invariante en el tiempo, la respuesta a

x[n] = Aδ[n-k] será Ah[n-k]

Esto nos permitirá conocer la respuesta a cualquier entrada arbitraria x[n] ya que siempre podemos expresar a x[n] como:

x[n] = ∑ Ak.δ[n-k]

Por lo tanto aplicando superposición:

y[n] = ∑ Ak.h[n-k]

Esto se conoce como convolución discreta o suma de convolución entre la entrada (definida por los Ak) y la respuesta impulsiva h[n]

y[n] = x[n]* h[n]

La convolución discreta tiene las siguientes propiedades:

1. Conmutatividad:

x[n]*y[n]= y[n]*x[n]

2. Asociatividad:

(x[n]*y[n]*w[n] = x[n]*(y[n]*w[n])

Esto es aplicable por ejemplo si queremos determinar la salida para la cascada de 2 sistemas con respuesta impulsiva h1[n] y h2[n] respectivamente. Esta propiedad permite concluir que el orden de colocación de los sistemas no es importante.

(x[n]* h1[n])*h2[n] =(x[n]* h2[n])*h1[n]

3. Distributividad:

(x[n]+y[n])*w[n] = x[n]*w[n] + y[n]*w[n]

Esta propiedad nos permite determinar la salida cuando la señal de entrada pasa

por dos sistemas conectados en paralelo.

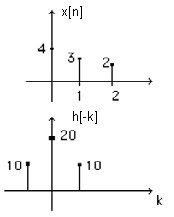
Ejemplo: Un sistema con respuesta h[n] es alimentado con una señal x[n], tal y como se muestra a continuación.

Determine la salida y[n] de dicho sistema mediante convolución.

Pasos para resolver la convolución discreta.

1.- Se cambia la variable n por k (x[n] →x[k]) y (h[n]→h[k]) y se refleja h[k] es decir h[-k]

2.- Se debe desplazar h[-k] n unidades, es decir, h[n-k], consiguiendo h[-(k-n)]

3.- Buscar los intervalos para los cuales x[k].h[n-k] = 0, para hallar el comienzo y fin de la convolución.

Para determinar estos valores se grafica dejando x[n] en su lugar y dibujando h[n-k] hacia la izquierda y derecha de x[n].

Como sigue a continuación:

Para que x[k].h[n-k] = 0, hacia la izquierda n+1<0

n < -1

Para que x[k].h[n-k] = 0, hacia la derecha n-1>2

n > 2+1

n>3

Por lo tanto, la convolución comenzará en n = -1 y terminará en n=3.

4.- Luego se deben multiplicar x[k].h[n-k], solo desplazando h[n-k] hacia la derecha. En este caso desde n= -1 hasta n = 3

Para n=-1

y[-1]= 4 x 10 = 40

Para n = 0

y[0]= 4 x 20 + 3 x 10= 110

Para n = 1

y[1]=4 x 10 + 3 x 20 + 2 x 10 = 120

Para n = 2

y[2]=3 x 10 + 2 x 20 = 70

Para n = 3

y[3]= 2 x 10= 20


Señal: y[n] = x[n]* h[n]